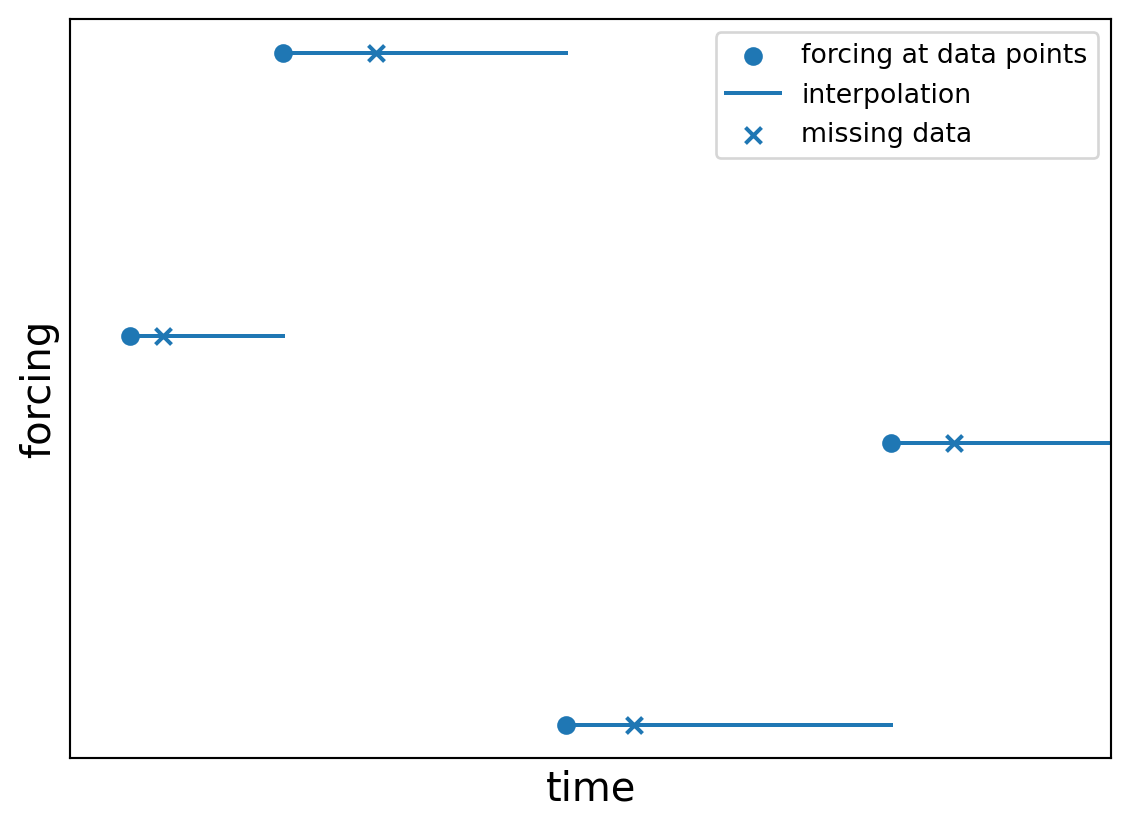
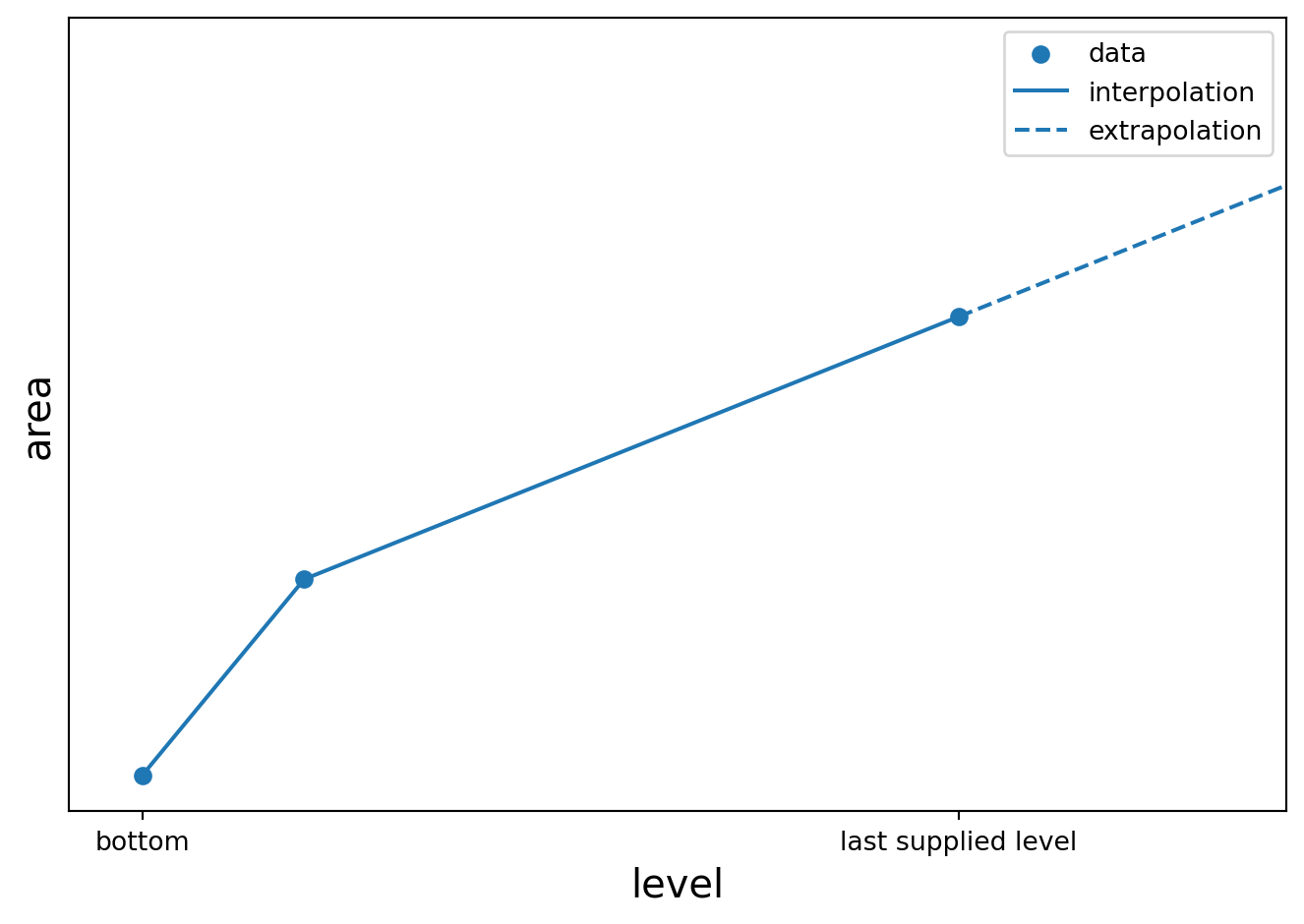
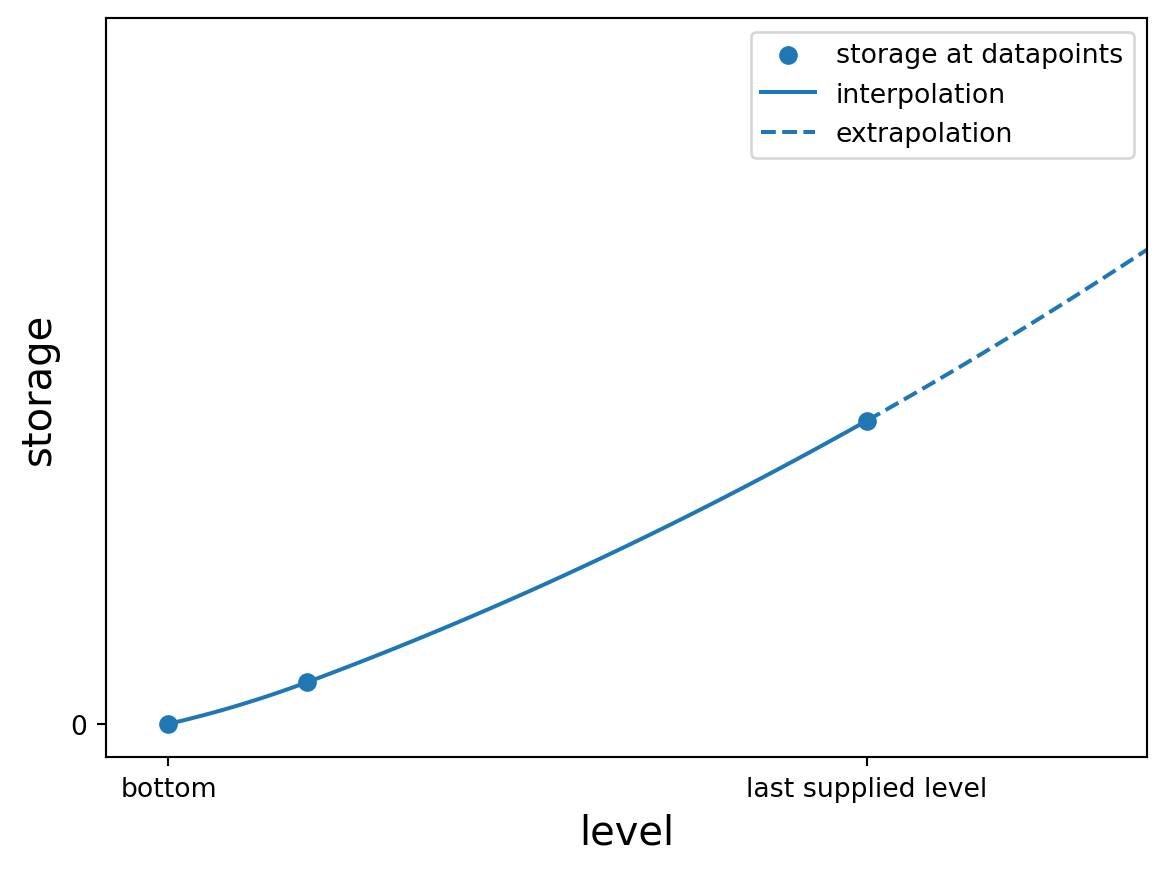
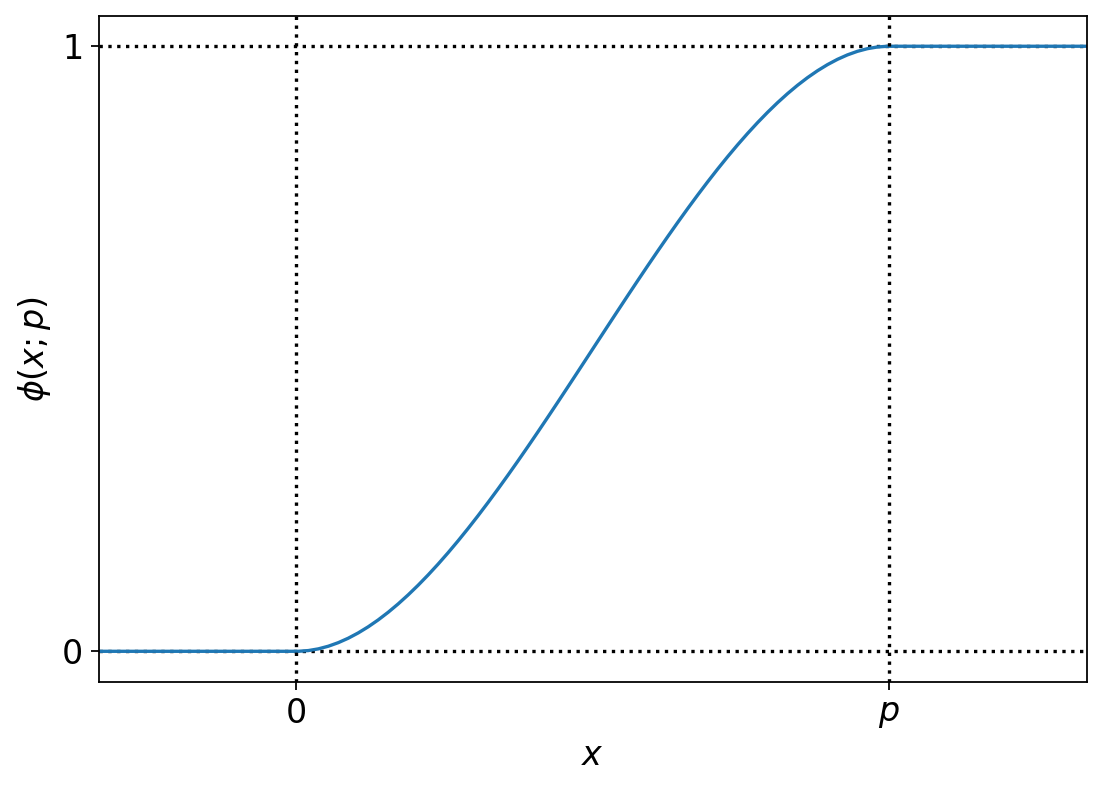
import plotly.graph_objects as go
import numpy as np
def linear_interpolation(X, Y, x, maximum):
i = min(max(0, np.searchsorted(X, x) - 1), len(X) - 2)
return min(Y[i] + (Y[i + 1] - Y[i]) / (X[i + 1] - X[i]) * (x - X[i]), maximum)
def A(h):
return linear_interpolation(level, area, h, maximum=area[-1])
fig = go.Figure()
x = area/2
x = np.concat([-x[::-1], x])
y = np.concat([level[::-1], level])
# Basin profile
fig.add_trace(
go.Scatter(
x = x,
y = y,
line = dict(color = "green"),
name = "Basin profile"
)
)
# Basin profile extrapolation
y_extrap = np.array([level[-1], level_extrap])
x_extrap = np.array([area[-1]/2, area_extrap/2])
fig.add_trace(
go.Scatter(
x = x_extrap,
y = y_extrap,
line = dict(color = "green", dash = "dash"),
name = "Basin extrapolation"
)
)
fig.add_trace(
go.Scatter(
x = -x_extrap,
y = y_extrap,
line = dict(color = "green", dash = "dash"),
showlegend = False
)
)
# Water level
fig.add_trace(
go.Scatter(x = [-area[0]/2, area[0]/2],
y = [level[0], level[0]],
line = dict(color = "blue"),
name= "Water level")
)
# Fill area
fig.add_trace(
go.Scatter(
x = [],
y = [],
fill = 'tonexty',
fillcolor = 'rgba(0, 0, 255, 0.2)',
line = dict(color = 'rgba(255, 255, 255, 0)'),
name = "Filled area"
)
)
# Create slider steps
steps = []
for h in np.linspace(level[0], level_extrap, 100):
a = A(h)
s = S(h).item()
i = min(max(0, np.searchsorted(level, h)-1), len(level)-2)
if h > level[-1]:
i = i + 1
fill_area = np.append(area[:i+1], a)
fill_level = np.append(level[:i+1], h)
fill_x = np.concat([-fill_area[::-1]/2, fill_area/2])
fill_y = np.concat([fill_level[::-1], fill_level])
step = dict(
method = "update",
args=[
{
"x": [x, x_extrap, -x_extrap, [-a/2, a/2], fill_x],
"y": [y, y_extrap, y_extrap, [h, h], fill_y]
},
{"title": f"Interactive water level <br> Area: {a:.2f}, Storage: {s:.2f}"}
],
label=str(round(h, 2))
)
steps.append(step)
# Create slider
sliders = [dict(
active=0,
currentvalue={"prefix": "Level: "},
pad={"t": 25},
steps=steps
)]
fig.update_layout(
title = {
"text": f"Interactive water level <br> Area: {area[0]:.2f}, Storage: 0.0",
},
yaxis_title = "level",
sliders = sliders,
margin = {"t": 100, "b": 100}
)
fig.show()